洛谷题单指南-最短路-P3403 跳楼机
原题链接:https://www.luogu.com.cn/problem/P3403
题意解读:三个正整数x,y,z,a、b、c都大于等于0,求1 + ax + by + cz在1 ~ h范围内所有可能的值的数量。
解题思路:
先将问题转化一下:求ax + by + cz在0 ~ h-1范围内所有可能的值的数量。
由于h范围很大,直接暴力枚举a,b,c显然不可取!
而x、y、z范围均不超过100000,ax + by + cz的值%x之后的范围是0 ~ x-1
因此,我们可以对可能值对x进行同余分组,也就是根据%x的余数将值分成x组。
同余最短路的思想就是把某一组值(%x相同的)作为图中的一个节点,然后找到并构建节点之间的关系,进而通过最短路的方式求解。
以样例来说明:h = 15,x = 4 y = 7 z = 9
1、对值%x的余数可能是0 ~ 3,因此定义图中有4个节点0 ~ 3
2、只需要求得每一种余数的数值数量,累加即可得到所有可能的值的数量
3、要求得每一种余数i的数值的数量,只需要知道这种余数的值中最小值di即可,该余数对应的数值的数量就是 (h - 1 - di) / x + 1
4、那么问题又变成了如果求每种余数的值的最小值
5、对于0号节点,也就是余数为0时,
如果加上y=7,余数会变成(0 + 7) % 4 = 3,因此可以在0->3之间连一条长度为7的边
如果加上z=9,余数会变成(0 + 9) % 4 = 1,因此可以在0->1之间连一条长度为9的边
6、对于1号节点,也就是余数为1时,
如果加上y=7,余数会变成(1 + 7) % 4 = 0,因此可以在1->0之间连一条长度为7的边
如果加上z=9,余数会变成(1 + 9) % 4 = 2,因此可以在1->2之间连一条长度为9的边
7、对于2号节点,也就是余数为2时,
如果加上y=7,余数会变成(2 + 7) % 4 = 1,因此可以在2->1之间连一条长度为7的边
如果加上z=9,余数会变成(2 + 9) % 4 = 3,因此可以在2->3之间连一条长度为9的边
8、对于3号节点,也就是余数为3时,
如果加上y=7,余数会变成(3 + 7) % 4 = 2,因此可以在3->2之间连一条长度为7的边
如果加上z=9,余数会变成(3 + 9) % 4 = 0,因此可以在3->0之间连一条长度为9的边
最终建图如下: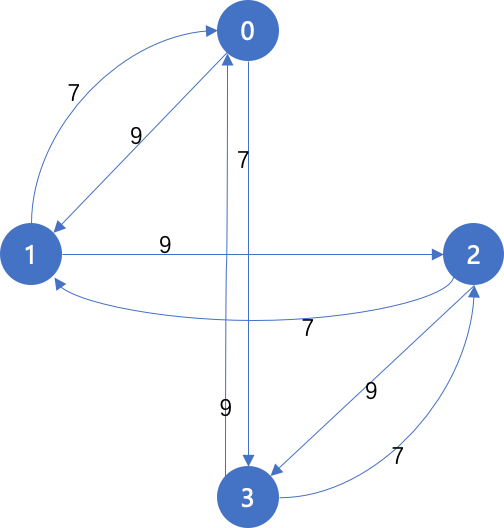
要求每种余数的值的最小值,其实就是求从0到各个节点的最短路:
d[0] = 0,对答案的贡献是(14 - 0) / 4 + 1 = 4
d[1] = 9,对答案的贡献是(14 - 9) / 4 + 1 = 2
d[2] = 14,对答案的贡献是(14 - 14) / 4 + 1 = 1
d[3] = 7,对答案的贡献是(14 - 7) / 4 + 1 = 2
因此,最终答案是4 + 2 + 1 + 2 = 9
根据以上分析,同余最短路的算法流程如下:
1、图中节点为0 ~ x - 1
2、针对每个节点i:0 ~ x - 1,从i - > (i + y) % x,i - > (i + z) % z分别连一条长度为y、z的边
3、从0开始跑一遍最短路,设i点的最短路为d[i]
4、最终答案为∑ (h - 1 - d[i]) / x + 1
注意:求得的最短路不能超过h - 1
100分代码:
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef pair<LL, int> PLI;
const int N = 100005, M = 2 * N;
int h[N], e[M], w[M], ne[M], idx;
LL H, ans, dist[N];
bool vis[N];
int x, y, z;
void add(int a, int b, int c)
{
e[++idx] = b;
w[idx] = c;
ne[idx] = h[a];
h[a] = idx;
}
void dijikstra()
{
memset(dist, 0x3f, sizeof(dist));
dist[0] = 0;
priority_queue<PLI, vector<PLI>, greater<PLI>> pq;
pq.push({0, 0});
while(pq.size())
{
PLI p = pq.top(); pq.pop();
int u = p.second;
if(vis[u]) continue;
vis[u] = true;
for(int i = h[u]; ~i; i = ne[i])
{
int v = e[i];
if(dist[v] > dist[u] + w[i])
{
dist[v] = dist[u] + w[i];
if(!vis[v]) pq.push({dist[v], v});
}
}
}
}
int main()
{
memset(h, -1, sizeof(h));
cin >> H >> x >> y >> z;
for(int i = 0; i < x; i++)
{
add(i, (i + y) % x, y);
add(i, (i + z) % x, z);
}
dijikstra();
for(int i = 0; i < x; i++)
if(H - 1 >= dist[i]) //注意不能超范围
ans += (H - 1 - dist[i]) / x + 1;
cout << ans;
return 0;
}
