洛谷题单指南-最小生成树-P3366 【模板】最小生成树
原题链接:https://www.luogu.com.cn/problem/P3366
题意解读:最小生成树概念和算法模版。
解题思路:
最小生成树(MST)是在一个连通的带权图中,找到一棵包含所有顶点且边权之和最小的树。常见的最小生成树算法有普里姆(Prim)算法和克鲁斯卡尔(Kruskal)算法,以下是对这两种算法的详细介绍:
一、Prim 算法
算法思想:从图中任意选择一个顶点作为起始顶点,将其加入到已访问顶点集合中。然后,不断从与已访问顶点相邻的未访问顶点中选择权值最小的边,将对应的未访问顶点加入到已访问顶点集合中,直到所有顶点都被访问到。
算法步骤:
初始化:选择一个起始顶点,将其标记为已访问,并将其到其他顶点的距离初始化为边权(若没有直接边,则距离为无穷大)。
寻找最小边:在所有未访问顶点中,找到与已访问顶点相邻且边权最小的顶点,将其标记为已访问,并将对应的边加入到最小生成树中。
更新距离:对于新加入的顶点,更新其相邻的未访问顶点到已访问顶点集合的距离。
重复步骤 2 和 3,直到所有顶点都被访问到,此时得到的树就是最小生成树。
算法图示:

把节点1加入最小生成树集合,集合内点为{1},同时用1更新其他点到集合的距离
然后找到不在集合中且距离集合最近的点和边1->2,加入集合,集合内点为{1,2},同时用2更新其他点到集合的距离
然后找到不在集合中且距离集合最近的点和边1->3,加入集合,集合内点为{1,2,3},同时用3更新其他点到集合的距离
最后找到不在集合中且距离集合最近的点和边1->4,加入集合,算法完毕。
时间复杂度:时间复杂度为 O(V^2),其中 V 是图的顶点数。如果使用堆等数据结构来优化寻找最小边的操作,时间复杂度可以优化到 O((V + E)log V),其中 E 是图的边数。
适用场景:适用于顶点数相对较少、边数较多的稠密图。
证明思路:通过反证法来证明 Prim 算法生成的树是最小生成树。假设存在一棵由 Prim 算法生成的树不是最小生成树,然后推出矛盾。
证明过程:
设图G=(V,E),其中V是顶点集,E是边集。Prim 算法从顶点u开始,逐步生成最小生成树T。
假设存在一棵最小生成树T’与 Prim 算法生成的树T不同,且在 Prim 算法执行过程中,第一次遇到的不属于T’的边为e=(v,w),其中v是已在T中的顶点,w是未在T中的顶点。
由于T’是最小生成树,那么在T’中一定存在一条从v到w的路径P,且路径P上一定存在一条边e’=(x,y),其中x在已加入T的顶点集合中,y不在。
因为 Prim 算法选择的是与已加入顶点集合相连的权值最小的边,所以w(e)<=w(e’)。如果将e’从T’中删除,加入e,得到的新树T’’的权值不会增加,即w(T’’)<=w(T’)。
这与T’是最小生成树且与T不同矛盾,所以 Prim 算法生成的树一定是最小生成树。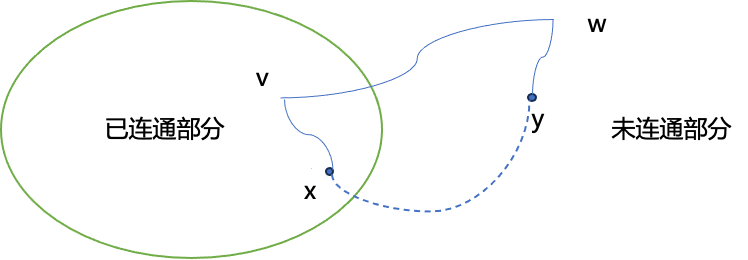
100分代码:
#include <iostream>
#include <cstring>
using namespace std;
const int N = 5005, INF = 0x3f3f3f3f;
int g[N][N];
bool vis[N]; //每个节点是否在最小生成树集合中
int dist[N]; //每个节点距离集合的距离
int n, m;
int ans = 0; //最小生成树的权值
bool prim()
{
memset(dist, 0x3f, sizeof(dist));
dist[1] = 0; //从节点1开始
for(int i = 1; i <= n; i++)
{
int t = 0; //集合之外距离集合最近的节点
for(int j = 1; j <= n; j++)
if(!vis[j] && (t == 0 || dist[j] < dist[t]))
t = j;
if(t == 0) break; //所有节点都在集合中
if(dist[t] == INF) return false; //如果选中的节点距离集合的距离为INF,说明图不连通
vis[t] = true; //将t加入集合
ans += dist[t]; //更新最小生成树的权值
for(int j = 1; j <= n; j++)
if(!vis[j]) dist[j] = min(dist[j], g[t][j]); //更新距离集合的距离
}
return true;
}
int main()
{
cin >> n >> m;
memset(g, 0x3f, sizeof(g));
while(m--)
{
int u, v, w;
cin >> u >> v >> w;
g[u][v] = g[v][u] = min(g[u][v], w);
}
if(prim()) cout << ans << endl;
else cout << "orz" << endl;
return 0;
}
二、Kruskal 算法
算法思想:将图中所有边按照权值从小到大进行排序,然后从权值最小的边开始,依次将边加入到最小生成树中。如果加入某条边会导致形成环,则不加入该边,直到所有顶点都被连接起来。
算法步骤:
初始化:将所有边按照权值从小到大排序,初始化一个空的最小生成树和一个并查集,用于判断顶点之间的连通性。
选择边:从排序后的边集合中选择权值最小的边,检查该边的两个顶点在并查集中是否属于同一个连通分量。如果不属于同一个连通分量,则将该边加入到最小生成树中,并将两个顶点所在的连通分量合并。
重复步骤 2,直到所有顶点都被连接起来,或者已经选择了 V - 1 条边(V 是顶点数),此时得到的树就是最小生成树。
算法图示: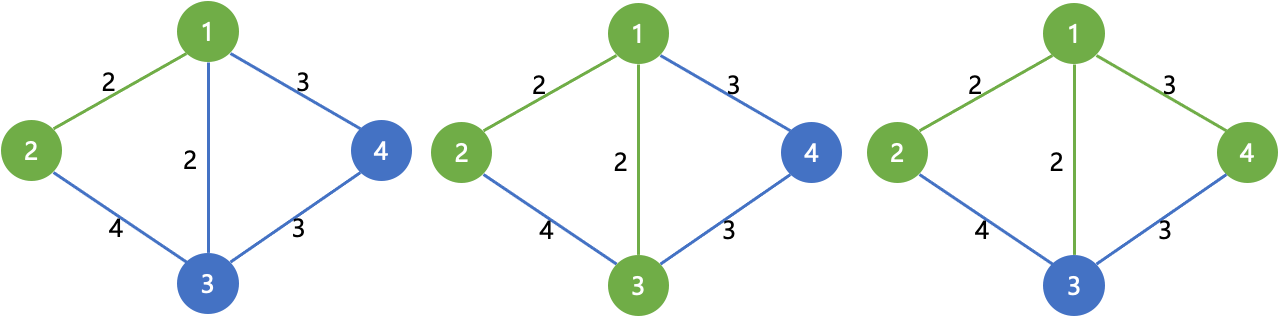
先对所有边权排序,枚举所有边
选取边权最小的1->2,将1,2用并查集连通
再选边1->3,将1,3用并查集连通
再选边1->4,将1,4用并查集连通
此时加入的边数为n-1,算法结束
时间复杂度:时间复杂度主要由边的排序和并查集操作决定,边排序的时间复杂度为 O(Elog E),并查集操作的时间复杂度为 O(1)。因此,Kruskal 算法的时间复杂度为 O(Elog E)。
适用场景:适用于边数相对较少、顶点数较多的稀疏图。
证明思路:同样使用反证法,假设 Kruskal 算法生成的树不是最小生成树,然后通过构造新的树来推出矛盾。
证明过程:
设图G=(V,E),Kruskal 算法将边按权值从小到大排序后,依次选择边加入生成树T。
假设存在一棵最小生成树T’与 Kruskal 算法生成的树T不同,设e是 Kruskal 算法选择的第一条不在T’中的边。
把e加入T’中,会形成一个环。由于T’是最小生成树,环上一定存在一条边e’,其权值大于等于e的权值(因为 Kruskal 算法是按权值从小到大选边的,如果存在一个e’<e的权值,则会先选择e’)。
从T’中删除e’,加入e,得到新的树T’’,其权值w(T’’)<=w(T’)。
这与T’是最小生成树且与T不同矛盾,所以 Kruskal 算法生成的树是最小生成树。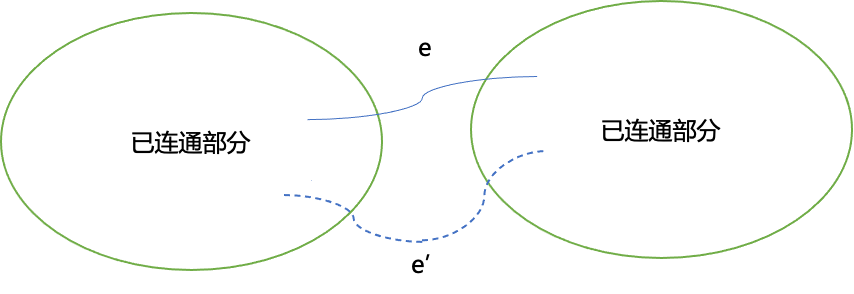
100分代码:
#include <iostream>
#include <algorithm>
using namespace std;
const int N = 5005, M = 400005, INF = 0x3f3f3f3f;
struct Edge
{
int u, v, w;
bool operator < (const Edge &e) const
{
return w < e.w;
}
} edges[M]; //边集数组
int p[N]; //并查集
int n, m;
int ans; //最小生成树的权值
int cnt; //最小生成树的边数
//查询x在集合中的根节点
int find(int x)
{
if(p[x] != x) p[x] = find(p[x]);
return p[x];
}
bool kruskal()
{
sort(edges + 1, edges + m + 1); //按边权值从小到大排序
for(int i = 1; i <= n; i++) p[i] = i; //并查集初始化
for(int i = 1; i <= m; i++)
{
int u = edges[i].u, v = edges[i].v, w = edges[i].w;
int a = find(u);
int b = find(v);
if(a != b) //如果u、v不连通
{
p[a] = b; //将u、v连通
ans += w; //加u->v加入最小生成树
if(++cnt == n - 1) return true;
}
}
return false;
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= m; i++)
cin >> edges[i].u >> edges[i].v >> edges[i].w;
if(kruskal()) cout << ans << endl;
else cout << "orz" << endl;
return 0;
}
