洛谷题单指南-树与图上的动态规划-P4316 绿豆蛙的归宿

原题链接：https://www.luogu.com.cn/problem/P4316

题意解读：有向图中，从一个点有k条出边，则从这k条边走的概率是1/k，求从起点到终点路径长度的数学期望。

解题思路：

1、数学期望

所谓数学期望，是一种均值，它是一个随机变量取值的加权平均，权重由该随机变量的概率分布决定。

假设我们有一个离散型随机变量 X，它的取值为 x₁, x₂, …, xₙ，并且每个取值的概率分别是 P (x₁), P (x₂), …, P (xₙ)，那么该随机变量的期望值 E [X] 定义为：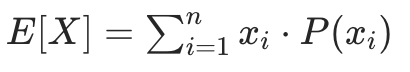

2、问题建模

设f[i]表示从i走到终点路径长度的数学期望，i有k条出边，对于i指向的所有节点j，有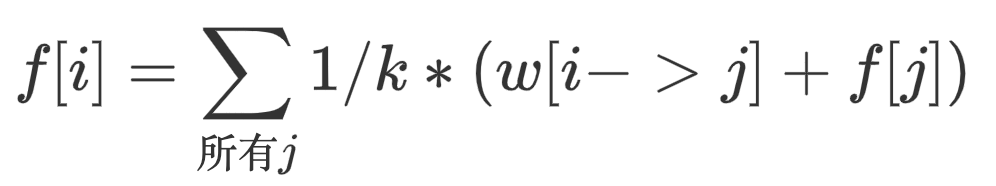

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 100005, M = 200005;

int head[N], to[M], w[M], nxt[M], idx;
int out[N]; //出度 
double dp[N]; //dp[i]表示从i走到终点路径长度的数学期望
int n, m;

void add(int a, int b, int c)
{
    to[++idx] = b;
    w[idx] = c;
    nxt[idx] = head[a];
    head[a] = idx;
    out[a]++;
}

double f(int u)
{
    if(u == n) return dp[n] = 0; //初始化终点
    if(dp[u]) return dp[u];
    for(int i = head[u]; i; i = nxt[i])
    {
        int v = to[i];
        dp[u] += 1.0 / out[u] * (w[i] + f(v));
    }
    return dp[u];
}

int main()
{
    cin >> n >> m;
    while (m--)
    {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
    }
    printf("%.2lf", f(1));
}