洛谷题单指南-连通性问题-P4819 [中山市选] 杀人游戏

原题链接：https://www.luogu.com.cn/problem/P4819

题意解读：在一个有向图中，选择最少的点，使得可以判断所有点是否是杀手，设最少的点数量为x，结果是1 - x/n。

解题思路：

显然，可以先进行缩点。

缩点后会出现三种情况：

1、不存在孤立点也不存在多余点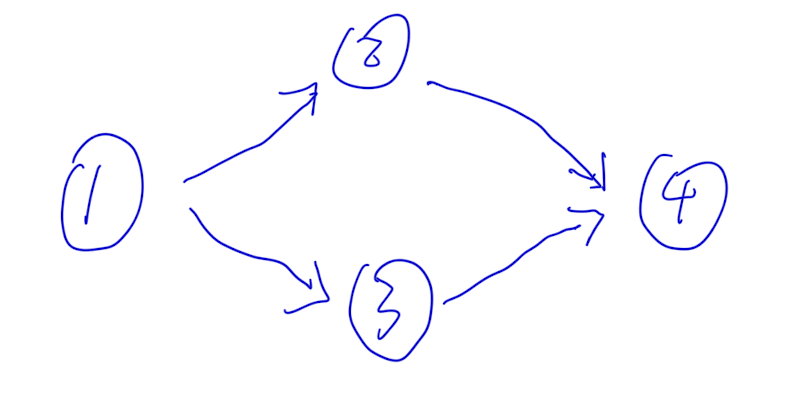

统计所有入度为0的缩点个数x，从每个缩点中选一个即可，答案为1 - x / n。

2、不存在孤立点且存在多余点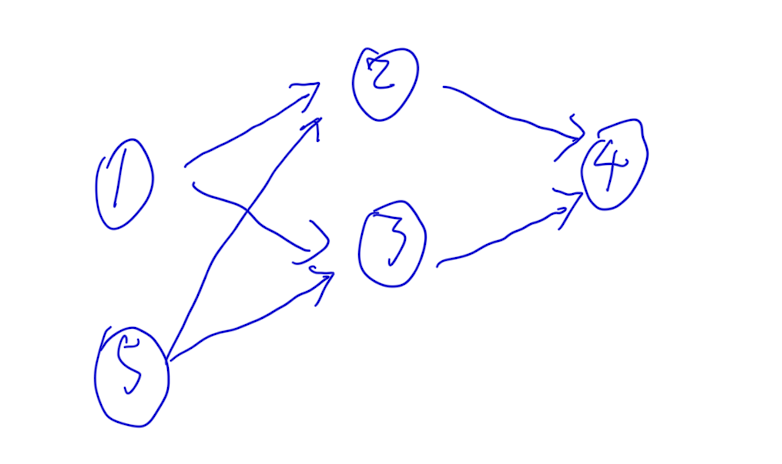

图中，从1可以走遍1、2、3、4，如果确定了1、2、3、4的情况，5就不言自明，这样5就是多余的点，这样的点的特点是：入度为0且所有指向的节点的入度都大于1。

注意5在缩点之前节点数也是1个。

这时答案为1 - (x - 1) / n。

3、存在孤立点

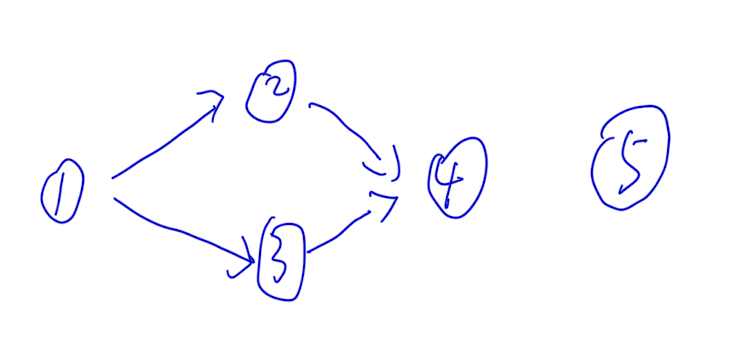
对于其中一个孤立点5，也是多余的，因为其他的点如果都判断过，孤立点的结果自然知晓（其他点中如果找到杀手，孤立点必然不是杀手；其他点中如果未找到杀手，孤立点中必然有杀手）。

注意5在缩点之前节点数也是1个。

这时答案为1 - (x - 1) / n。

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 100005, M = 300005;
int head[N], to[M], nxt[M], idx; //原图
vector<int> g[N]; //缩点图
int dfn[N], low[N], timestamp;
stack<int> stk;
bool vis[N];
int scc[N], sz[N], cnt;
int in[N], out[N]; //缩点后入度、出度
int n, m;
map<pair<int, int>, int> mp;

void add(int a, int b)
{
    to[++idx] = b;
    nxt[idx] = head[a];
    head[a] = idx;
}

void tarjan(int u)
{
    dfn[u] = low[u] = ++timestamp;
    stk.push(u);
    vis[u] = true;
    for(int i = head[u]; i; i = nxt[i])
    {
        int v = to[i];
        if(!dfn[v])
        {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if(vis[v]) low[u] = min(low[u], dfn[v]);
    }
    if(low[u] == dfn[u])
    {
        cnt++;
        while(true)
        {
            int t = stk.top(); stk.pop();
            vis[t] = false;
            scc[t] = cnt;
            sz[cnt]++;
            if(t == u) break;
        }
    }
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= m; i++)
    {
        int u, v;
        cin >> u >> v;
        add(u, v);
    }

    for(int i = 1; i <= n; i++)
        if(!dfn[i])
            tarjan(i);

    for(int u = 1; u <= n; u++)
    {
        for(int i = head[u]; i; i = nxt[i])
        {
            int v = to[i];
            int a = scc[u], b = scc[v];
            if(a != b)
            {
                if(mp.count({a, b})) continue; //判重边
                mp[{a, b}] = 1;
                out[a]++;
                in[b]++;
                g[a].push_back(b);
            }
        }
    }

    bool flag = false;
    int x = 0;
    for(int u = 1; u <= cnt; u++)
    {
        if(!in[u]) 
        {
            x++;
            if(sz[u] == 1)
            {
                if(!out[u]) flag = true; //孤立点
                else
                {
                    int ok = true;
                    for(auto v : g[u])
                    {
                        if(in[v] <= 1) 
                        {
                            ok = false; //只有有一个邻点的入度小于等于1
                            break;
                        }
                    }
                    if(ok) flag = true;
                }
            }   
        }
    }

    if(flag) printf("%.6f", 1 - 1.0 * (x - 1) / n);
    else printf("%.6f", 1 - 1.0 * x / n);

    return 0;
}