洛谷题单指南-连通性问题-P3469 [POI 2008] BLO-Blockade

原题链接：https://www.luogu.com.cn/problem/P3469

题意解读：无向图中，计算经过每一个节点的路径条数，路径长度至少是1。

解题思路：

要计算经过节点的路径条数，在树中是比较好处理的，无非三种形式：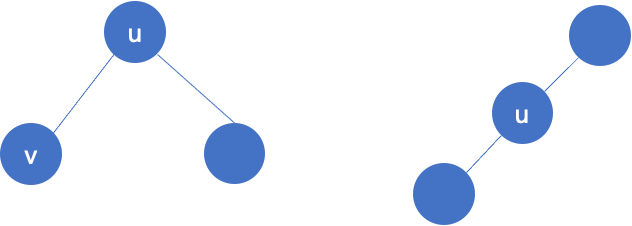

左图：经过u点的路径两端都在u的子树上，枚举u的子树，用子树v的大小乘以其余子树的大小，然后求和，即是经过u的路径数
右图：经过u点的路径两端只有一个在u的子树上，用子树u的大小乘以剩余节点数（减1除去u本身），即使经过u的路径数
其他：u点到其他所有点都有一条路径，路径数为2 * (n-1)
因此，可以把无向图转化成圆方树，类似https://www.cnblogs.com/hackerchef/p/18857808

但是，如果对点双连通分量的本质进一步剖析，可以发现，在tarjan遍历出的dfs生成树中，同样可以做类似处理,

只不过，这里变量到点u，在计算子树大小时，要分情况：

影响连通性的情况：这才相当于树中的节点，才应该计算子树大小

不影响连通性的情况：不纳入计算子树大小

因此计算子树大小时要分情况，具体在代码中体现。

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 100005;

vector<int> g[N];
int dfn[N], low[N], timestamp;
bool cut[N];
int sz[N]; //子树大小
long long ans[N];
int n, m;

void tarjan(int u, int p)
{
    dfn[u] = low[u] = ++timestamp;
    sz[u] = 1;
    int sum = 0; //sum是u是影响连通性的点时子树的大小
    for(auto v : g[u])
    {
        if(v == p) continue;
        if(!dfn[v])
        {
            tarjan(v, u);
            sz[u] += sz[v];
            low[u] = min(low[u], low[v]);

            if(low[v] >= dfn[u]) //不存在回边，u影响连通性，不一定是割点，也可能是根节点
            {
                ans[u] += 2ll * sz[v] * sum;
                sum += sz[v]; //影响连通性的u的子树大小要单独算
            }
        }
        else low[u] = min(low[u], dfn[v]);
    }
    ans[u] += 2ll * sum * (n - sum - 1); //u如果是根节点，sum=n-1；u如果是非割点，sum=0
    ans[u] += 2ll * (n - 1);
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i <= m; i++)
    {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    tarjan(1, 0);
    for(int i = 1; i <= n; i++)
        cout << ans[i] << endl;
    return 0;
}