洛谷题单指南-连通性问题-P1656 炸铁路(无向图的双连通分量,割边、割点)
原题链接:https://www.luogu.com.cn/problem/P1656
题意解读:求无向图中所有的割边。
解题思路:
本题开始学习无向图的双连通性,在此之前建议先学习有向图的强连通性相关知识:https://www.cnblogs.com/hackerchef/p/18851009
一、基本概念
- 连通性 (Connectivity)
连通图:无向图中任意两个顶点之间都存在路径相连。如果图中存在多个互不连通的子图,则称为非连通图。
连通分量:无向图中的极大连通子图。对于连通图,整个图本身就是一个连通分量;对于非连通图,则包含多个连通分量。
- 双连通性 (Biconnectivity)
双连通性分为两种类型,分别针对边和顶点的删除:
(1) 边双连通性 (Edge Biconnectivity)
定义:一个连通无向图如果删除任意一条边后仍然保持连通,则称为边双连通图。
关键概念:
割边/桥 (Bridge):割边也称为桥,在无向图中,如果移除某条边后,图的连通分量数量增加,那么这条边就被称为割边。
边双连通分量:极大边双连通子图(不包含任何桥的极大子图)
内部连通性:在一个边双连通分量中,任意两个顶点之间都至少存在两条边不重复的路径。
极大性:无法再向该分量中添加其他顶点和边,使其成为更大的边双连通子图。
缩点性质:如果将每个边双连通分量看作一个 “缩点”,那么原图就可以转化为一棵由这些缩点组成的树(如果原图是连通的),树中的边就是原图中的割边。
(2) 点双连通性 (Vertex Biconnectivity)
定义:一个连通无向图如果删除任意一个顶点(及其关联边)后仍然保持连通,则称为点双连通图。
关键概念:
割点:在无向图中,若移除某个顶点以及与之相连的所有边后,图的连通分量数量增加,那么这个顶点就被称为割点。
点双连通分量:极大点双连通子图
内部连通性:点双连通分量内任意两点之间至少存在两条点不重复的路径。
极大性:无法向该分量中添加其他顶点和边以构成更大的点双连通子图。
割点的特殊性:两个不同的点双连通分量最多只有一个公共顶点,且这个公共顶点是原图中的割点。若两个点双连通分量有多个公共顶点,那么删除其中一个顶点后,这两个分量仍能保持连通,这与点双连通分量的定义不符,所以公共顶点只能是割点。
缩点性质:将每个点双连通分量看作一个 “缩点”,同时将原图中的割点保留,可得到一个新的图结构。在这个新结构中,割点连接着不同的点双连通分量缩点,呈现出一种类似树状的结构(如果原图是连通的),不过与边双连通分量缩点后得到的严格树形结构有所不同,这里割点可能会连接多个缩点。
边的特性:点双连通分量中的边具有这样的特点,对于任意一条边,其两个端点必然在同一个点双连通分量中。而且,若删除该边,不会影响该分量内其他顶点之间的点双连通性。
二、求割边和边双连通分量
1、算法原理
求解边双连通分量和割边通常采用 Tarjan 算法,其核心思想基于深度优先搜索(DFS)。在 DFS 过程中,为每个顶点记录两个重要信息:
dfn[u]:u的DFS序号
low[u]:u通过树边和回边(不能走指向父节点的边)能追溯到的最小的dfn值
对于一条边u->v,若low[v] > dfn[u],则u->v是割边。
这是因为从v及其子孙节点无法通过其他路径回到u或其祖先节点,所以删除u->v会使图的连通性改变。
求边双连通分量有两种方法:
可以将所有割边删除,再在图中进行dfs求出所有边双连通分量
更简单的做法是类似求强联通分量,用栈保存dfs中的节点,在回溯时,如果low[u] == dfn[u],说明u是当前栈中节点双连通分量的根,对堆栈进行处理即可。
注意:在求边双连通分量时,由于是无向图,不存在方向问题,一条边的两个端点可以互相到达,只需要找到割边,然后在原图上将割边屏蔽进行遍历(不能往回走),每次找到的连通块就是一个边双连通分量,不需要判断节点是否在堆栈中。
2、缩点流程
使用 Tarjan 算法求出所有边双连通分量和割边。
如果两个边双连通分量之间存在割边,则在缩点后的图中连接它们。
最终形成一棵树(或森林,如果原图不连通)。
3、代码示例
void tarjan(int u, int p)
{
dfn[u] = low[u] = ++timestamp;
stk.push(u);
for(int i = head[u]; i; i = nxt[i])
{
int v = to[i];
if(v == p) continue; //不能往回走
if(!dfn[v])
{
tarjan(v, u);
low[u] = min(low[u], low[v]);
if(low[v] > dfn[u]) //找到割边
{
bridge.push_back({min(u, v), max(u, v)});
}
}
else
{
low[u] = min(low[u], dfn[v]);
}
}
if(low[u] == dfn[u]) //找到双连通分量的起点
{
cnt++;
while(true)
{
int t = stk.top(); stk.pop();
ebcc[t] = cnt;
if(t == u) break;
}
}
}
三、求割点和点双连通分量
1、算法原理
Tarjan 算法是求解无向图割点和点双连通分量的经典算法,基于深度优先搜索(DFS)实现。在 DFS 过程中,为每个顶点维护两个重要信息:
dfn[u]:u的DFS序号
low[u]:u通过树边和回边(不能走指向父节点的边)能追溯到的最小的dfn值
对于顶点u,判断其是否为割点的规则如下:
如果u是根节点(DFS 树的根),且u有至少两个子节点,那么u是割点。
如果u不是根节点,且存在一个子节点v使得low[v] >= dfn[u],那么u是割点。这是因为从v及其子孙节点出发,无法通过回边到达u的祖先节点(不包括u本身)。也就是说,一旦去掉u这个顶点,v及其子孙节点就会与图的其他部分断开联系,导致图的连通分量数量增加,所以u是割点。
在 DFS 过程中,使用栈来记录访问的边,这是因为不同的点双连通分量可以有相同的割点,不能把点归到某一个点双连通分量,但是一个点双连通分量中边是唯一的。实际操作时,只需要记录访问到的点,当发现割点时,从栈中弹出点,直到遇到当前割点的子节点,这些点加上当前割点构成一个点双连通分量,弹栈后割点还要保留在栈中,以访问包含这个割点的其他点双连通分量。
注意:求点双连通分量时,通常是通过判断割点来确定。在无向图的深度优先搜索中,通过维护一个父节点指针p来避免重复访问父节点导致的错误判断,而不需要借助堆栈来判断节点是否在某个特定的集合中。
2、缩点流程
使用 Tarjan 算法求出所有点双连通分量和割点。
如果割点u属于某个点双连通分量B,则在缩点后的图中连接u和B。
最终形成一棵树(或森林,如果原图不连通)。
3、代码示例
void tarjan(int u, int p)
{
dfn[u] = low[u] = ++timestamp;
stk.push(u);
int child = 0;
for(int i = head[u]; i; i = nxt[i])
{
int v = to[i];
if(v == p) continue;
if(!dfn[v])
{
child++;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u]) //找到割点u
{
if(p != 0 || child >= 2) //u不是根节点:直接判定割点 u是根节点:子节点大于2才是割点
cut[u] = true;
//栈到u的点都是点双连通分量,但弹栈只到v,因为u还是其他连通分量的割点
cnt++;
vbcc[cnt].push_back(u); //割点肯定属于点双连通分量,但不能从栈中弹出
while(true)
{
int t = stk.top(); stk.pop();
vbcc[cnt].push_back(t);
if(t == v) break; //弹栈一直到v,都属于一个点双连通分量
}
}
}
else low[u] = min(low[u], dfn[v]);
}
}
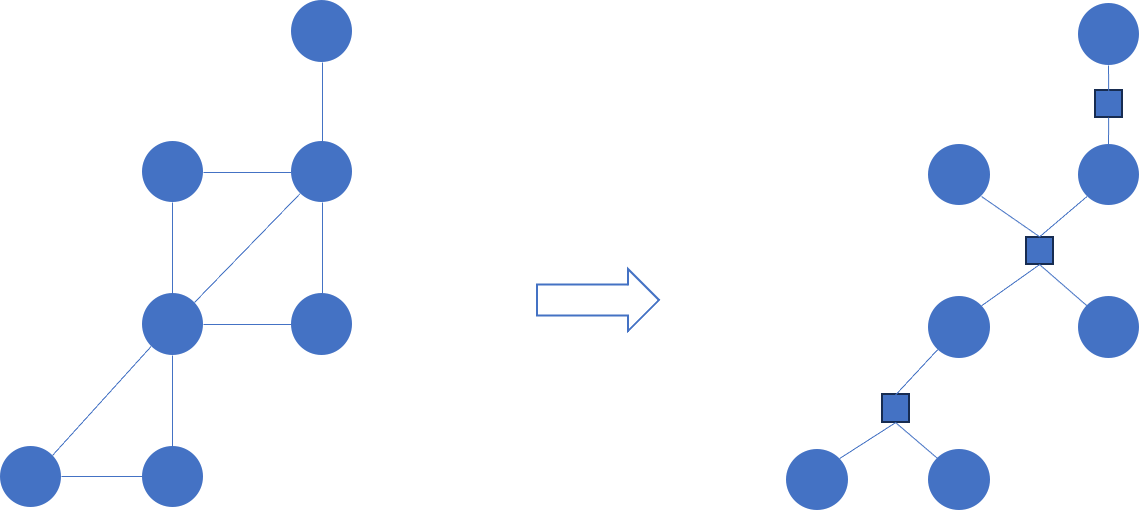
4、圆方树
将原图中的点称为圆点,代表电双连通分量的点称为方点,那么这样的一棵树形结构被称为圆方树。圆方树的建立只需要在找到割点以及点双连通分量时,将当前点双连通分量代表的点编号记为cnt+n,再建立cnt+n到所有电双连通分量中点的边。
这样一来,
圆方树中,所有割点都是度大于1的点,所有方点的度就是所代表点双连通分量的大小。
每个点双连通分量形成一个“菊花图”,多个“菊花图”通过原图中的割点连接在一起。
回到本题,只需要求割边即可。
100分代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 155, M = 5005;
int head[N], to[M], nxt[M], idx = 1; //idx=1,也就是编号从2开始是为了便于通过idx^1判得到反向边
int dfn[N], low[N], timestamp;
stack<int> stk;
vector<pair<int, int>> bridge; //保存所有割边
//int ebcc[N], cnt; //标记节点属于哪个边双连通分量
int n, m;
void add(int a, int b)
{
to[++idx] = b;
nxt[idx] = head[a];
head[a] = idx;
}
void tarjan(int u, int p)
{
dfn[u] = low[u] = ++timestamp;
stk.push(u);
for(int i = head[u]; i; i = nxt[i])
{
int v = to[i];
if(v == p) continue; //不能往回走
if(!dfn[v])
{
tarjan(v, u);
low[u] = min(low[u], low[v]);
if(low[v] > dfn[u]) //找到割边
{
bridge.push_back({min(u, v), max(u, v)});
}
}
else
{
low[u] = min(low[u], dfn[v]);
}
}
/*
if(low[u] == dfn[u]) //找到双连通分量的起点
{
cnt++;
while(true)
{
int t = stk.top(); stk.pop();
ebcc[t] = cnt;
if(t == u) break;
}
}
*/
}
int main()
{
cin >> n >> m;
for(int i = 1; i <= m; i++)
{
int u, v;
cin >> u >> v;
add(u, v), add(v, u);
}
for(int i = 1; i <= n; i++)
if(!dfn[i])
tarjan(i, 0);
sort(bridge.begin(), bridge.end());
for(auto p : bridge) cout << p.first << " " << p.second << endl;
return 0;
}
