洛谷题单指南-连通性问题-P4606 [SDOI2018] 战略游戏

原题链接：https://www.luogu.com.cn/problem/P4606

题意解读：连通的无向图，给出若干个询问，每个询问是一组点，求图中有多少个点删去会造成这组点不连通。

解题思路：

1、问题分析

对于询问中的一组点，可以构建其最小连通的子图（也就是树），就是要求这棵树中所有的点数再减去已知的点数。

对于图中一组点，构造的树，称为虚树（https://oi-wiki.org/graph/virtual-tree/）

比如：已知点是4、6、7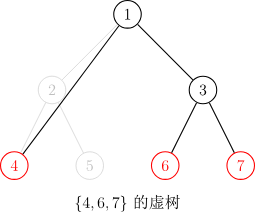

但本题与虚树有所不同，对于已知点4、6、7，最小连通的树涉及的节点包括：4、2、1、3、6、7

那如何要求得最小连通树的节点数呢？

2、算法流程

由于原图不易处理，可以先将无向图转化成圆方树；

点权不易处理，可以转成边权，圆点的父边权值为1，方点的父边权值为0；

将已知点按DFN排序，再两两求lca，累加每相邻两点到lca的距离之和，最后再累加首项和末项到lca的距离，除以2，就得到最小连通树除根节点外的节点个数，根节点就是首项和末项的lca，如果根节点是圆点，节点数再加1，方点则忽略。

如此即可算出一组点的最小连通树中所有节点的个数，减去已知点的个数即得到答案。

举例说明以上计算过程：

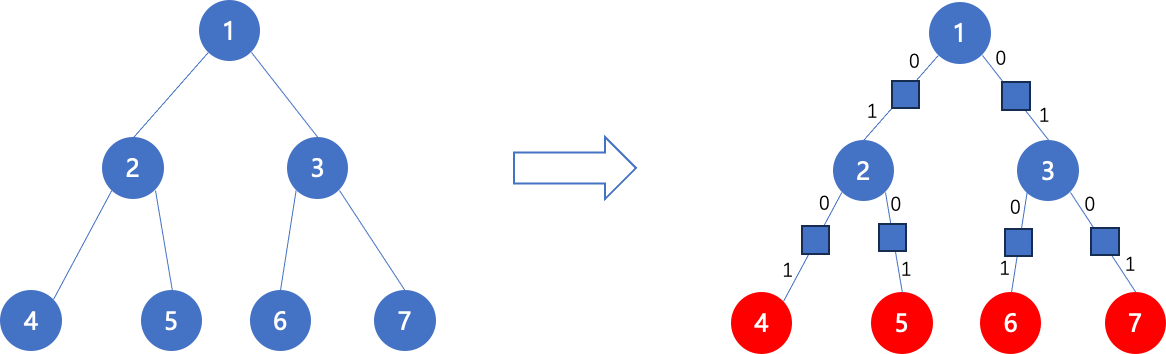
如图，已知点4,5,6,7

先将点按dfn排序，得到4,5,6,7

求4、5的lca，是2，4、5到2的距离之和为2，ans += 2

求5、6的lca，是1，5、6到1的距离之和为4，ans += 4

求6、7的lca，是3，6、7到1的距离之和为2，ans += 2

求4、7的lca，是1，4、7到1的距离之和为4，ans += 4

此时ans = 12，ans / 2 = 6，再看根节点1是圆点，因此ans = 7

最后，减去已知点数ans = 7 - 4 = 3，正好是1,2,3三个点的数量

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 200005, M = 800005;
int head1[N], head2[N], to[M], nxt[M], idx; //head1:原图 head2:圆方树
int dfn[N], low[N], timestamp;
int stk[N], top;
int cnt; //点双个数
int dist[N]; //圆方树中到根节点的距离
int depth[N], fa[N][18]; //圆方树中节点深度、第2^i个父节点信息
int a[N]; //一次询问中已占领的点
int t, n, m;

bool cmp(int x, int y)
{
    return dfn[x] < dfn[y];
}

void add(int head[], int a, int b)
{
    to[++idx] = b;
    nxt[idx] = head[a];
    head[a] = idx;
}

void tarjan(int u, int p)
{
    dfn[u] = low[u] = ++timestamp;
    stk[++top] = u;
    for(int i = head1[u]; i; i = nxt[i])
    {
        int v = to[i];
        if(v == p) continue;
        if(!dfn[v])
        {
            tarjan(v, u);
            low[u] = min(low[u], low[v]);

            if(low[v] >= dfn[u])
            {
                cnt++;
                add(head2, cnt + n, u), add(head2, u, cnt + n); //圆方树建边
                while(true)
                {
                    int t = stk[top--];
                    add(head2, cnt + n, t), add(head2, t, cnt + n); //圆方树建边
                    if(t == v) break;
                }
            }
        }
        else low[u] = min(low[u], dfn[v]);
    }
}

void dfs(int u, int p)
{
    dfn[u] = ++timestamp;
    depth[u] = depth[p] + 1;
    dist[u] = dist[p] + (u <= n); //当前节点是圆点距离+1，当前节点是方点距离+0
    fa[u][0] = p;
    for(int i = 1; i < 18; i++)
    {
        fa[u][i] = fa[fa[u][i - 1]][i - 1];
    }
    for(int i = head2[u]; i; i = nxt[i])
    {
        int v = to[i];
        if(v == p) continue;
        dfs(v, u);
    }
}

int lca(int u, int v)
{
    if(depth[u] < depth[v]) swap(u, v);
    for(int i = 17; i >= 0; i--)
    {
        if(depth[fa[u][i]] >= depth[v])
        {
            u = fa[u][i];
        }
    }
    if(u == v) return u;
    for(int i = 17; i >= 0; i--)
    {
        if(fa[u][i] != fa[v][i])
        {
            u = fa[u][i];
            v = fa[v][i];
        }
    }
    return fa[u][0];
}

void clear()
{
    memset(head1, 0, sizeof(head1));
    memset(head2, 0, sizeof(head2));
    memset(dfn, 0, sizeof(dfn));
    memset(low, 0, sizeof(low));
    idx = 0, top = 0, cnt = 0, timestamp = 0;
}

int main()
{
    cin >> t;
    while(t--)
    {
        clear();
        cin >> n >> m;
        for(int i = 1; i <= m; i++)
        {
            int u, v;
            cin >> u >> v;
            add(head1, u, v), add(head1, v, u);
        }
        tarjan(1, 0); //建立圆方树
        timestamp = 0; 
        dfs(1, 0); //dfs重新计算dfn,预处理lca相关数组,以及到根节点的距离
        int q;
        cin >> q;
        while(q--)
        {
            int s;
            cin >> s;
            for(int i = 1; i <= s; i++) cin >> a[i];
            sort(a + 1, a + s + 1, cmp); //已占领点按dfn排序

            int ans = 0;
            for(int i = 1; i < s; i++)
            {
                int u = a[i], v = a[i + 1], l = lca(u, v);
                ans += dist[u] + dist[v] - 2 * dist[l];
            }
            int u = a[1], v = a[s], l = lca(u, v);
            ans += dist[u] + dist[v] - 2 * dist[l];
            ans = ans / 2 + (l <= n) - s;
            cout << ans << endl;
        }
    }
    return 0;
}