洛谷题单指南-连通性问题-P4630 [APIO2018] 铁人两项

原题链接：https://www.luogu.com.cn/problem/P4630

题意解读：在无向图中，选取在一条简单的不走重复点的路径上的s、c、f三个点，求方案数。

解题思路：

1、问题分析

如果固定两点s、f，此时的方案数就是s到f路径上的点的个数减2（除去s、f自身）。

普通的无向图不容易处理，而圆方树刚好有一个神奇的特性：如果方点权值为其点双连通分量大小、圆点权值为-1，那么两个圆点之间路径的点权值之和，正好就是原图中两个点所有简单路径上的点的个数减2。

基于这个特性，我们只需要对圆方树中的圆点枚举s、f，然后求路径权值之和。

直接枚举时间复杂度过高，换一个角度，枚举所有的点(圆点和方点)，求有多少条经过该点的路径，然后该点对答案的贡献就是2权值路径数。

乘2是因为两个方向是不同方案；

对于经过一个点的路径数，在树上有两种可能：

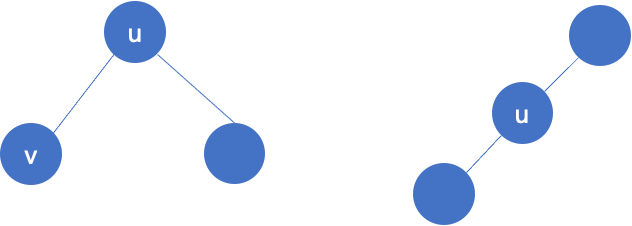
经过u点的路径两端都在u的子树上，枚举u的子树，用子树v的大小乘以其余子树的大小，然后求和，即是经过u的路径数
经过u点的路径两端只有一个在u的子树上，用子树u的大小乘以剩余节点数，即使经过u的路径数
通过一次DFS即可求解。

2、算法流程**

构建圆方树，同时记录圆方树中节点个数
DFS每个点，求每个点对答案的贡献
注意图不一定连通

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 100005, M = 200005;

int head1[N], head2[N * 2], to[M * 3], nxt[M * 3], idx; //head1：原图 head2：圆方树
int dfn[N], low[N], timestamp;
stack<int> stk;
int cnt; //点双的个数
int w[N * 2]; //圆方树的点权值，方点是点双的大小，圆点是-1
int sz[N * 2]; //圆方树中节点的子树大小
int total; //圆方树一个连通块的大小
long long ans;
int n, m;

void add(int head[], int a, int b)
{
    to[++idx] = b;
    nxt[idx] = head[a];
    head[a] = idx;
}

void tarjan(int u, int p)
{
    total++;
    dfn[u] = low[u] = ++timestamp;
    stk.push(u);
    for(int i = head1[u]; i; i = nxt[i])
    {
        int v = to[i];
        if(v == p) continue;
        if(!dfn[v])
        {
            tarjan(v, u);
            low[u] = min(low[u], low[v]);

            if(low[v] >= dfn[u])
            {   
                cnt++; //找到点双
                add(head2, n + cnt, u), add(head2, u, n + cnt); //圆方树建边
                w[u] = -1; //圆点权值
                int size = 1;
                while(true)
                {
                    int t = stk.top(); stk.pop();
                    size++;
                    add(head2, n + cnt, t), add(head2, t, n + cnt); //圆方树建边
                    w[t] = -1; //圆点权值
                    if(t == v) break;
                }
                w[n + cnt] = size; //方点权值
            }
        }
        else low[u] = min(low[u], dfn[v]);
    }
}

void dfs(int u, int p)
{
    if(u <= n) sz[u] = 1; //子树大小只计算圆点
    for(int i = head2[u]; i; i = nxt[i])
    {
        int v = to[i];
        if(v == p) continue;
        dfs(v, u);
        ans += 2ll * sz[v] * sz[u] * w[u]; //点u作为中点，s、f分别在子树中
        sz[u] += sz[v];
    }
    ans += 2ll * sz[u] * (total - sz[u]) * w[u]; //点u作为中点，s、f一个在子树中
}

int main()
{
    cin >> n >> m;
    for(int i = 1;i <= m; i++)
    {
        int u, v;
        cin >> u >> v;
        add(head1, u, v), add(head1, v, u);
    }

    for(int i = 1; i <= n; i++)
    {
        if(!dfn[i])
        {
            total = 0;
            tarjan(i, 0);
            dfs(i, 0);
        }
    }


    cout << ans;
    return 0;
}