洛谷题单指南-连通性问题-P5025 [SNOI2017] 炸弹

原题链接：https://www.luogu.com.cn/problem/P5025

题意解读：

解题思路：

1、问题分析

首先，要看到一个重要的事实：一个炸弹能覆盖的其他炸弹一定是一个连续的区间，因此一个炸弹能引爆一系列的炸弹也是一个连续的区间。

在一个炸弹和其可以引爆的炸弹之间，建立一条有向边，即可形成有向图，节点是炸弹的编号。

通过对有向图求强联通分量，并缩点反向建图，形成DAG，根据拓扑序进行递推，可以求得每一个缩点能都走到的最小、最大的节点编号。

每个炸弹能引爆的炸弹数就是炸弹所在缩点能走到的最大编号 - 最小编号 + 1。

但是：问题关键在于建图，对于一个炸弹可能引爆n个炸弹，这样建图时空复杂度都将是O(n^2)。

2、线段树优化建图

这里介绍一种通过线段树来优化建图的手段，可以将建图的空间复杂度优化到O(nlogn)，时间复杂度优化到O(n)

假设一个图有6个节点，要建立6到1~5的有向边，常规方法是这样的：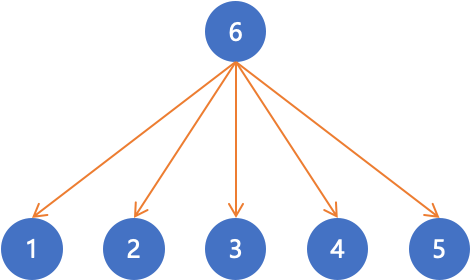

也就是一共要建n-1条边。

如果先用线段树来维护6个节点，并且将线段树的节点也建立有向图，那么要建立6到1~5的有向边，只需要这样操作：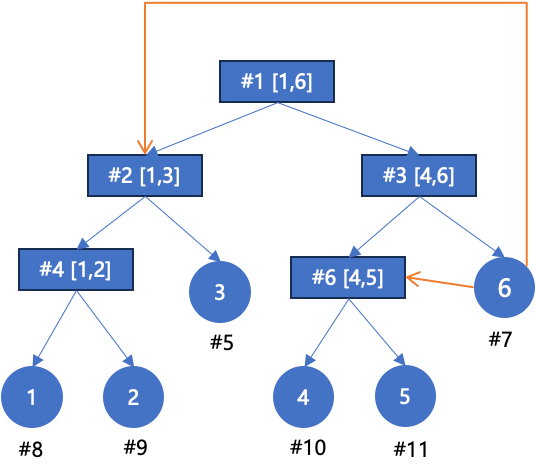

建边的条数一下就降到logn了，建边也类似一个区间更新操作，不用一个点一个点的建边。

最终整个线段树的节点之间就形成了有向图，其连通关系与传统方式建立的图是一致的，也就是如果6最终能走到1~5，那么在线段树建图中也是同样的。

3、算法流程

首先对所有节点建立线段树，同时构建有向图
根据炸弹覆盖范围与范围内[l,r]的炸弹建立有向边，通过线段树区间操作完成
对有向图通过tarjan求强联通分量
缩点建反向图
拓扑排序，递推
计算并输出结果
100分代码：

#include <bits/stdc++.h>
using namespace std;

typedef long long ll;
const int N = 500005, MOD =  1e9 + 7;

ll x[N], r[N];

//建图相关
int head1[N * 4], head2[N * 4], to[N * 40], nxt[N * 40], idx;
int maxn; //最大节点编号

//线段树相关
struct Node
{
    int l, r; //线段树节点tr[u]表示从节点u能到到达的炸弹编号范围是tr[u].l~tr[u].r
} tr[N * 4];
int id[N]; //炸弹编号对应的线段树节点编号

//tarjan相关
int dfn[N * 4], low[N * 4], timestamp;
stack<int> stk;
bool vis[N * 4];

//连通分量相关
int cnt; //连通分量数
int scc[N * 4]; //节点对应的连通分量
int lid[N * 4]; //每个连通分量缩点能到的最小编号
int rid[N * 4]; //每个连通分量缩点能到的最大编号
int in[N * 4]; //连通分量缩点的入度

int n;

void add(int head[], int a, int b)
{
    to[++idx] = b;
    nxt[idx] = head[a];
    head[a] = idx;
}

void build(int u, int l, int r)
{
    tr[u] = {l, r};
    if(l == r) id[l] = u, maxn = max(maxn, u); //图中节点对应的线段树节点，线段树最大节点编号
    else
    {
        int mid = l + r >> 1;
        build(u << 1, l, mid), build(u << 1 | 1, mid + 1, r);
        add(head1, u, u << 1), add(head1, u, u << 1 | 1); //建边
    }
}

void update(int u, int s, int l, int r)
{
    if(tr[u].l >= l && tr[u].r <= r) //节点表示的炸弹的范围在l~r范围内
    {
        add(head1, s, u);
    }
    else if(tr[u].l > r || tr[u].r < l) return;
    else
    {
        update(u << 1, s, l, r);
        update(u << 1 | 1, s, l, r);
    }
}

void tarjan(int u)
{
    dfn[u] = low[u] = ++timestamp;
    stk.push(u);
    vis[u] = true;
    for(int i = head1[u]; i; i = nxt[i])
    {
        int v = to[i];
        if(!dfn[v])
        {
            tarjan(v);
            low[u] = min(low[u], low[v]);
        }
        else if(vis[v]) low[u] = min(low[u], dfn[v]);
    }
    if(low[u] == dfn[u])
    {
        cnt++;
        while(true)
        {
            int t = stk.top(); stk.pop();
            vis[t] = false;
            scc[t] = cnt;
            lid[cnt] = min(lid[cnt], tr[t].l); //更新连通分量能到的最小炸弹编号
            rid[cnt] = max(rid[cnt], tr[t].r); //更新连通分量能到的最大炸弹编号
            if(t == u) break;
        }
    }
}

void topsort()
{
    queue<int> q;
    for(int i = 1; i <= cnt; i++)
    {
        if(!in[i]) q.push(i);
    }
    while(q.size())
    {
        int u = q.front(); q.pop();
        for(int i = head2[u]; i; i = nxt[i])
        {
            int v = to[i];
            lid[v] = min(lid[v], lid[u]);
            rid[v] = max(rid[v], rid[u]);
            if(--in[v] == 0)
            {
                q.push(v);
            }
        }
    }
}

int main()
{
    memset(lid, 0x3f, sizeof(lid));
    cin >> n;
    for(int i = 1; i <= n; i++) cin >> x[i] >> r[i];
    //基于线段树建立初始图
    build(1, 1, n);

    //建立每个炸弹与能引爆范围炸弹的关系
    for(int i = 1; i <= n; i++)
    {
        ll lpos = x[i] - r[i]; //当前炸弹能覆盖的最左坐标
        ll rpos = x[i] + r[i]; //当前炸弹能覆盖的最右坐标
        int lno = lower_bound(x + 1, x + n + 1, lpos) - x; //当前炸弹能覆盖的最左炸弹编号
        int rno = upper_bound(x + 1, x + n + 1, rpos) - x - 1; //当前炸弹能覆盖的最右炸弹编号
        update(1, id[i], lno, rno); //基于线段树建边，注意炸弹编号转成线段树的节点编号
    }

    //tarjan求强联通分量
    tarjan(1); //根据线段树的性质，#1一定能到所有节点

    //缩点，反向建图，便于递推
    for(int u = 1; u <= maxn; u++)
    {
        for(int i = head1[u]; i; i = nxt[i])
        {
            int v = to[i];
            int a = scc[u], b = scc[v];
            if(a != b) //两个连通分量有边a->b
            {
                add(head2, b, a); //反向建图
                in[a]++;
            }
        }
    }

    //拓扑序递推
    topsort();

    //计算结果
    ll ans = 0;
    for(int i = 1; i <= n; i++)
    {
        ans += 1ll * i * (rid[scc[id[i]]] - lid[scc[id[i]]] + 1);
        ans %= MOD;
    }
    cout << ans;

    return 0;
}